Modeling Solubility Behavior of CO2 in [C2-mim][BF4] and [C4-mim][BF4] Ionic Liquids by sPC-SAFT Equation of State

1. Introduction

Ionic liquids (ILs) are organic salts that are liquids at room temperature, including at least one large and asymmetric organic cation or anion.  ILs have unique properties such as negligible vapor pressure, good thermal stability, and capability to remain liquid over 300 K. Because of these  advantages ILs have many different applications and in comparison to other solvents ILs can be used for capturing greenhouse gases such as CO₂ [1].

In order to use ILs for capturing CO₂, thermodynamic models must be available to calculate the solubility of CO₂ in ILs. Different authors model the solubility of gases in ILs with equation of states (EOS) at different thermodynamic conditions; however, some EOS, such as the classical cubic EOS because of its simplicity, they do not take into account the effect of polarity and hydrogen bonding of ILs in an explicit manner [2]. In addition, these kinds [3] of model have some limitations: the critical parameters needed are not available for ILs, most of ILs tend to degrade before reaching the critical point [3]

Recently, statistical associating fluid theory (SAFT) EOS [4, 5] have also been used for modeling of CO₂ solubility in ILs [6, 7]. In the 1990s, studies led to different versions of the equation with different acronyms such as tPC-PSAFT [6, 8, 9], SAFT-VR [10], hetero-SAFT [11], PCP-SAFT [12], soft-SAFT [7, 13, 14] and, later, PC-SAFT [15]. Kroon, et al. [8] used the tPC-PSAFT equation of state to study the phase behaviour of ionic liquid + CO2 systems. Llovell, et al. [16] used the soft-SAFT equation to estimate the thermodynamic properties of pure ILs and mixtures containing ILs. Also, Andreu and Vega [7, 13] checked the ability of the soft-SAFT EOS to describe the solubility of CO₂ in ionic liquids. Paduszynski, et al. [12] used PCP-SAFT EOS for modelling systems with ionic liquids.

           In this work, the simplified perturbed chain statistical associating fluid theory (sPC-SAFT) was used to model systems containing ILs. EOS parameters for ILs were estimated by fitting available experimental liquid density data over a wide range of temperatures and atmospheric pressures. Furthermore, the model was utilized and extended for modeling phase behavior of imidazolium based ILs + CO₂ systems.

2. Model Description

2.1. PC-SAFT Modeling

         After Chapman, et al. [4] who introduced the SAFT EOS based on Wertheim’s first order thermodynamic perturbation theory [17], in 2001 the PC-SAFT EOS was developed by Gross and Sadowski [15, 16, 18]

         PC-SAFT model has received a lot of attention because this model can predict and correlate different thermodynamic properties of a great variety of simple and complex molecular systems [19]. They derived a dispersion expression for chain molecules and used a hard-chain reference fluid. Then, Von Solms, et al. [20] simplified this equation of state (sPC-SAFT) by introducing average diameter of segments in the mixture and simplifying the radial distribution function of mixture. They replaced the radial distribution function of mixture by radial distribution function of the pure component.

          The sPC-SAFT equation is usually written in terms of the residual Helmholtz free energy. The equation is given by:

(1)

 where a^res is the dimensionless residual Helmholtz free energy  of the system. The superscripts hc, disp, and assoc refer to a reference hard-chain contribution, a dispersion contribution, and an associating contribution, respectively.

The hard chain contribution to the Helmholtz free energy is defined by Gross and Sadowski [15, 18] as

(2)

The Helmholtz free energy of the hard-sphere fluid and the radial distribution function of the hard-sphere fluid are defined as:

	(3)
	(4)

Equations (3) and (4) obtained by the assumption of Von Solms, et al. [20] that all of the segments in the mixture have the same diameter.

In equations (3) and (4)  represents a reduced segment density

(5)

and  is the mean segment number

(6)

 a^disp  is based on expanding the second-order perturbation theory of  Barker and Henderson [21] to chain molecules.

The perturbation contribution is the sum of the first-and second-order term, according to

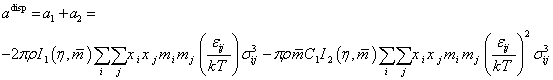(7)

In these equations, the integrals of the perturbation theory are substituted by simple power series in density of sixth order                      

	(8)
	(9)

Where the coefficients of the power series in density a_i and b_i depend on the chain length according to:

	(10)
	(11)

The universal model constants for the above equations are given in literature [15]

Conventional combining rules for ε_ij and σ_ij were employed

	(12)
	(13)

Where k_ij is the binary interaction parameter

The Helmholtz free energy due to association is defined by Huang and Radosz as [5, 22]:

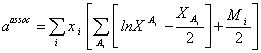(14)

Where  is the number of association sites per molecule, and  is the mole fraction of molecules i not bonded at site A. The parameter  is calculated from

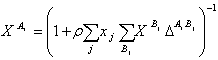(15)

 The association strength is given by

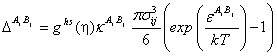(16)

where  is the effective association volume and  is the association energy.

3. Results and Analysis

3.1. Pure Components.

In this work in the sPC-SAFT framework, ILs were considered as neutral ion paires, and they were considered  as molecule.[7,8,13]. To describe specific interaction because of the charge and asymmetry of ILs molecules, an association site was considered on the ILs Molecule.

The sPC-PSAFT EOS has three parameters for non-associating compounds i.e., the segment number (m_i), the segment hard-sphere diameter (σ_i) and dispersion energy parameter (ε/k_B), and two additional parameters for association compounds i.e., the association energy (), and the association volume ().

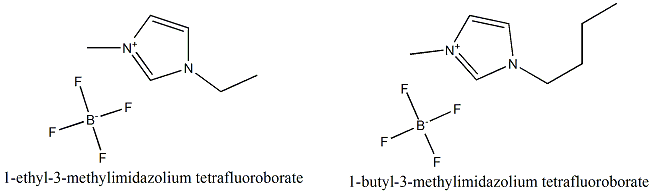
Tow imidazolium based ILs ie. 1-ethyl-3-methylimidazolium tetrafluoroborate [C₂-mim][BF₄] and 1-buthyl-3-methylimidazolium tetrafluoroborate [C₄-mim][BF₄] were used in this work. Figure 1 demonstrates chemical structures of the investigated ILs.

Figure 1. Chemical structure of the 1-ethyl-3-methylimidazolium tetrafluoroborate and 1-butyl-3-methylimidazolium tetrafluoroborate

In the first step, the ILs were considered as non-associating compounds. Three parameters m, σ, and ε/k_B were obtained by fitting liquid density data of ILs at atmospheric pressure. Table 1. shows the obtained parameters for the ILs studied in this work and percent average absolute relative error (AARE %) are provided. Good agreement with the experimental density data is observed.

In the second step, the ILs were considered as self-association compounds. To reduce the number of parameters that are fitted to experimental density data at atmospheric pressure, the values of association parameters were kept constant. They were teken from reference [] and only three non-associating parameters of pure imidazolium based ionic liquids were estimated. [C₂-mim][BF₄] and [C₄-mim][BF₄] were modelled using different association scheme according to terminology of Huang and Radosz [5, 22].

Table 2 shows the molecular parameters and AARE % in the density at atmospheric pressure. However, as the number of association site increases, more accuracy is shown. So, the best model with the minimum error is 10C (5 electron donor sites and 5 electron acceptor sites on ILs) and the ARRE% is 0.308% for 1-ethyl-3-methylimidazolium tetrafluoroborate ([C₂-mim][BF₄]) and 0.311% for 1-butyl-3-methylimidazolium tetrafluoroborate ([C₄-mim][BF₄]).

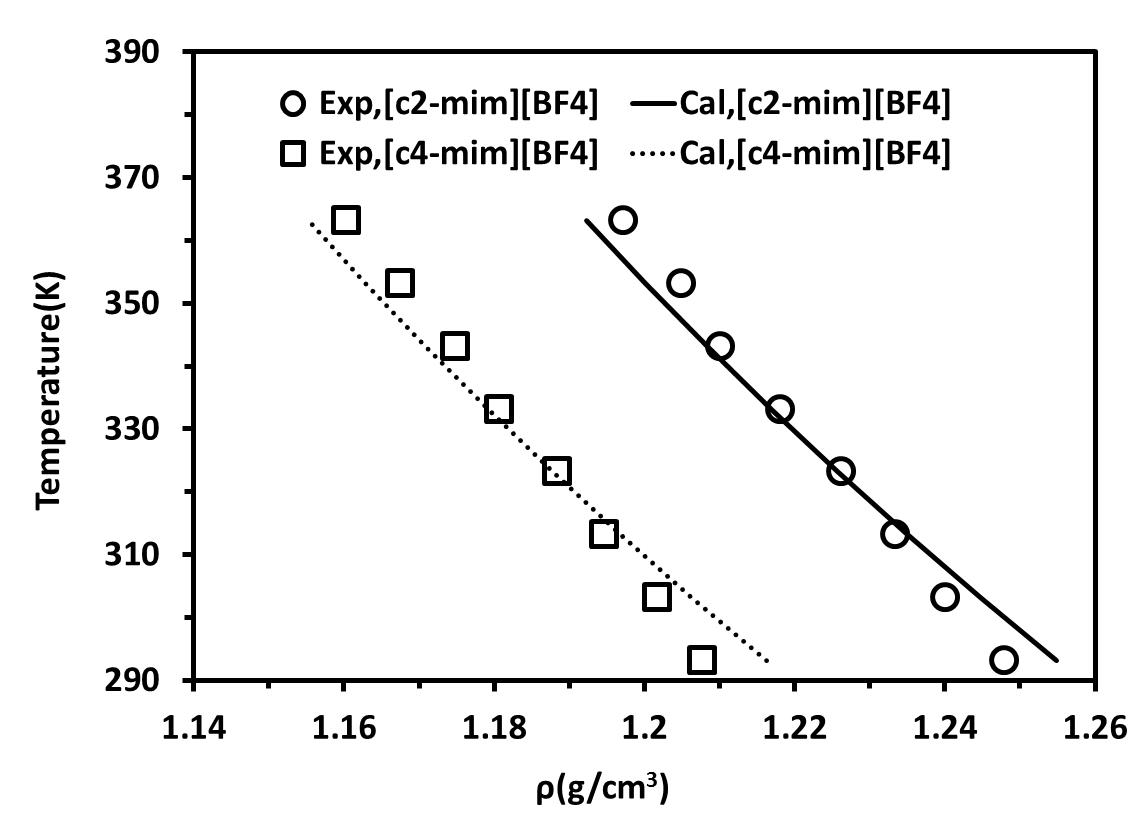
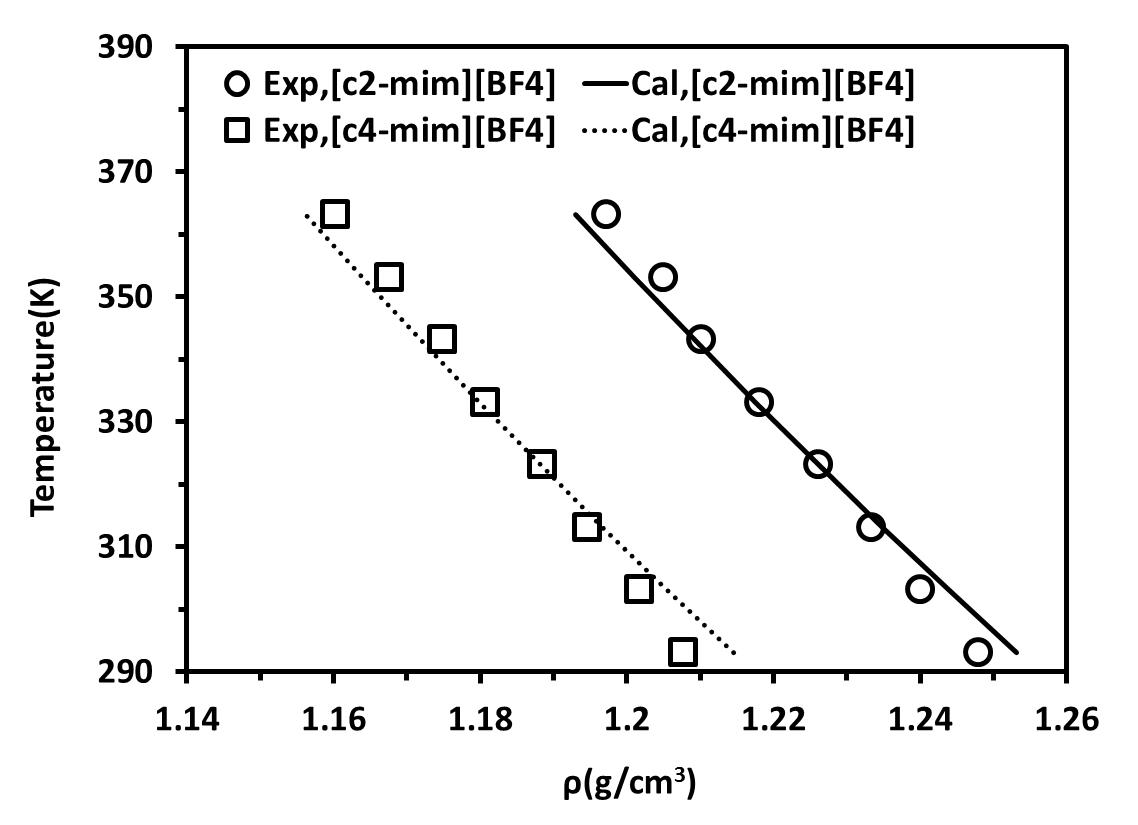
The resulting density− temperature diagrams at atmospheric pressure are shown in Figures 2a and 2b for the [C₂-mim][BF₄] and [C₄-mim][BF₄]. In Figure 2a ILs were considered as non-associating compound and in Figure 2b ILs were modelled using the 10C association scheme.

(17)

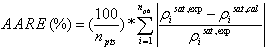Table 1. Optimized sPC-SAFT Parameters of Pure ILs Considered As Non-Associating Compounds and AARE% in density of ILs at atmospheric pressure

 Table 2. Optimized sPC-SAFT Parameters of Pure ILs Considered As Self-Associating Molecules and AARE% in density of ILs at atmospheric pressure

(a)	(b)
Figure 2. density-Temperature diagrams for ILs at atmospheric pressure.(a) ILs considered as non-associating compounds and (b) ILs considered as self-associating compounds with 10C association scheme

         After obtaining parameters at atmospheric pressure these parameters were used to predict the density of these two ILs at high pressure. Tables 3 and 4 present the AARE % between experimental and calculated liquid densities of these two  ILs at wide range of temperatures and high pressures up to 60 MPa for non-association and self-associating compound with 10C association scheme, respectively. Figures 3a and 3b show density- Pressure diagrams for self-associating and non-associating compounds at high pressure up to 60 MPa respectively. The results show t good agreement with the experimental data.

Table 3. AARE% in liquid density of pure ILs considered as Non-Associating Compounds at high pressure

Table 4. AARE% in liquid density of pure ILs considered as Self-Associating Molecules with 10C association scheme at high pressure

(a)	(b)
Figure 3. density- Pressure diagrams for [C4mim][BF4] at different temperature and high pressure.(a) considered as non-associating compounds, (b) considered as self-associating compounds with 10C association scheme

3.2. Mixtures:Solubility of CO₂ in [C₂-mim][BF₄] and [C₄-mim][BF₄] ionic liquids

                 After tuning paratemrs of sPC-SAFT EOS for ILs, these parameters were tested against prediction/correlation of solubility of CO₂ in these two ILs. CO₂ was considered as a non-associating molecule. Parameters for CO₂ were adapted from the literature [15]

                 We first studied the mixture {[C₂mim][BF₄]+CO₂} at pressures up to 5 MPa and at three different temperatures :T= 323.15-343.15 K. Figure 4 shows the solubility isotherms obtained for these mixtures as compared to experimental data [25]. It is obvious to see the accuracy of these calculations at low pressures as compared to the experimental data. Within the same family, we studied {[C₄mim][BF₄]+CO₂} at five different temperatures between 323.15-368.15. As shown in Figure 5, good agreement between the experimental data and the calculated values can be observed at low pressure.

              A comparison between Tables 5 and 6 shows that when association term is used, the solubility of carbon dioxide in these ILs increases and a higher accuracy is shown. Another comparison between low and high pressure is shown in Tables 5-7. High accuracy in correlation of solubility of CO₂ in ILs is shown when association term is used.

The results presented show that the sPC-SAFT model can be used to predict with high accuracy the phase diagrams of these ionic liquids with carbon dioxide. However, as shown in Table 7 a small deviation is observed at high pressure when mole fraction of CO₂ is greater than 0.5.

Table 5. AARE% in bubble point pressures for the different systems as Non-Associating Compounds at low pressures

Table 6. AARE% in bubble point pressures for the different systems as Self-Associating Molecules with 10C association scheme at low pressures

Table 7. AARE% in bubble point pressures for CO2+ [C₄mim][BF₄] at high pressures

         The values for the binary interaction parameter, k_ij, were initially fitted at various temperatures.  As shown in Figures 6a and 6b, the binary interaction parameters vary linearly with temperature according to the equation 18. The values of all parameters C₁ and C₂ are given in Tables 8 and 9 for non-association and association scheme, respectively.

(18)

Table 8. Binary interaction parameter temperature dependence for non-Associating Molecules

Table 9. Binary interaction parameter temperature dependence for Self-Associating Molecules with 10C association scheme  

         Finally, in order to realize the precision of our work compared to others, the  results were compared to some models in the literature. Figure 7 shows the density- Pressure diagrams for  [C₄mim][BF₄] considered as self-associating compounds with 10C association scheme at T=323.15 compared to Curras, et al [24]. Our result is more accurate than  experimental data obtained in  Curras et al. [24]  Figure 8 shows CO₂ solubility in [C₄mim][BF₄] compared to Ashrafmansouri and Raeissi [30] at T=333.15 . In this case, our result is close  to experimental data and slightly better than  Ashrafmansouri and Raeissi [30].

Figure 8. CO2 solubility in [C4mim][BF4] as self-associating compounds with 10C association scheme compared to Ashrafmansouri and Raeissi at T=333.15

4. Conclusion

sPC-SAFT EOS was used for 1-ethyl-3-methylimidazolium tetrafluoroborate and 1-butyl-3-methylimidazolium tetrafluoroborate to check the capability of this model to correlate solubility of CO₂ in these ILs in a wide range of temperatures and pressures.  Results were  compared to available experimental data. In this model, molecular parameters of pure ILs were estimated from experimental liquid density data over a wide range of temperatures at atmospheric pressure, good agreement with the experimental data is obtained at both atmospheric and high pressure.Then, solubility of carbon dioxide in ILs was studied. The binary interaction parameter is highly temperature-dependent and changes linearly with temperature. Finally, at  specific temperatures, the results were compared to other authors and good agreement with better accuracy was observed.

Acknowledment

         The authors gratefully acknowledge the National Iranian Gas Company- Parsian Gas Refining Company for their financial support of this MSc thesis by finance number 936010, date: 4-5-1393.